スイッチング電源の制御安定性
コンバータ解析の始め方 第3回
目次
はじめに
前回は、時比率$D$を入力とした際の降圧型コンバータの伝達関数を導出して、そのボード線図を確認しました。
確認した特性はコンバータ部であり、制御部の伝達関数は考えていません。
今回は、降圧型コンバータの出力を制御する補償器の作成と、補償器を含めた伝達関数について考えてみましょう。
▼ 前回:スイッチング電源電源解析のための伝達関数
補償器について
補償器は主に、主回路が常に目標とする値を出力できるように調整することを目的とします。
しかし、現実の回路では、周囲環境や接続先の負荷などの様々な要因によって出力は目標値とはなりません。
そのため、目標の出力となるように、入力を変化させるような補償器が必要となります。
補償器の設計
今回は補償器としてPID制御を考えます。
PID制御の一般的な伝達関数は、以下の式で表されます。
$$H(s) = K_p + K_i \frac{1}{s} + K_ds$$
ここで、積分項と微分項にカットオフ周波数$Fi$, $Fd$を持たせ、マスターゲイン$Km$を導入すると、以下の式に変換できます。
$$\begin{aligned}
H(s) &= K_m \big( K_p + K_i \frac{a}{s+a} + K_d \frac{s}{s+b} \big)
\\a &= 2 \pi F_i
\\b &= 2 \pi F_d
\end{aligned}$$
では、上記の伝達関数を確認してみましょう。
PID制御の各パラメータをそれぞれ以下の値とします。
| 変換名 | 値 | |
|---|---|---|
| 1 | マスターゲイン Km | 1 |
| 2 | 比例ゲイン Kp | 1 |
| 3 | 積分ゲイン Ki | 100 |
| 4 | 微分ゲイン Kd | 5 |
| 5 | 積分カットオフ周波数 Fi | 10 [Hz] |
| 6 | 積分カットオフ周波数 Fd | 10 [Hz] |
上記の変数はScideamのアナログPIDブロックの設定に遵守します。
前回同様、Python用のコードを使用して、ボード線図を確認しましょう。この時、動作周波数Fswは100[kHz]とします。
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import numpy as math
Km = 1
Kp = 1
Ki = 100
Kd = 5
fi = 10
fd = 10**4
a = 2 * math.pi * fi
b = 2 * math.pi * fd
num_p = Kp
sp = 1
num = [(Kp+Kd)*Km, (Kp*(a+b)+Kd*a+Ki*a)*Km, (Kp*a*b + Ki*a*b)*Km]
den = [1,a+b,a*b]
FRA_PID = signal.TransferFunction(num, den)
freq = np.logspace(-1, 9, 10000)
w, mag, phase = signal.bode(FRA_PID,2*np.pi*freq)
plt.figure(figsize=(8,8))
plt.subplot(2,1,1)
plt.xlim(0.1, 2e9)
plt.semilogx(freq, mag)
plt.ylabel('Gain [dB]')
plt.grid(True, which='both', axis='x', linestyle='--', linewidth=0.25, color='gray')
plt.grid()
plt.subplot(2,1,2)
plt.xlim(0.1, 2e9)
plt.semilogx(freq, phase)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Phase [deg]')
plt.grid(True, which='both', axis='x', linestyle='--', linewidth=0.25, color='gray')
plt.grid()
plt.show()
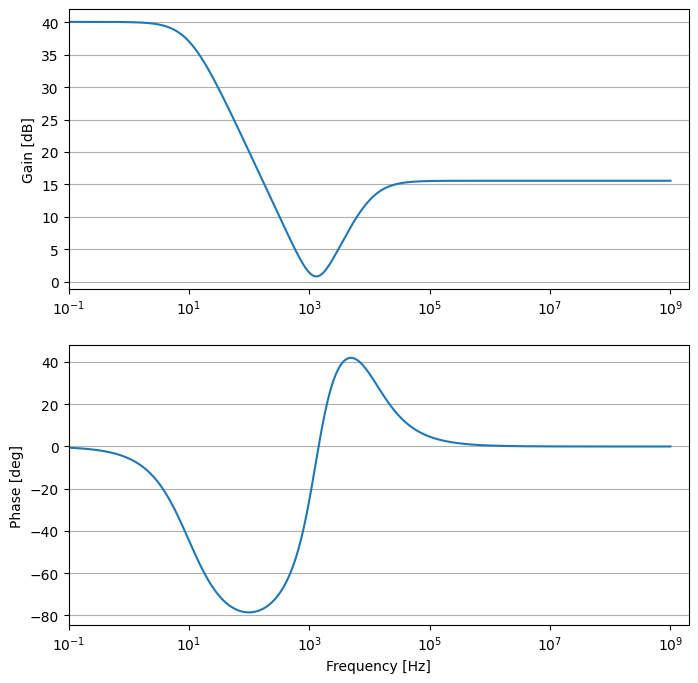
伝達関数から、ボード線図が得られましたので、ScideamのアナログPIDブロックを使用した場合のボード線図と比較してみましょう。
インスペクターに値を入力すると、解析を行わずともボード線図を確認することができます。
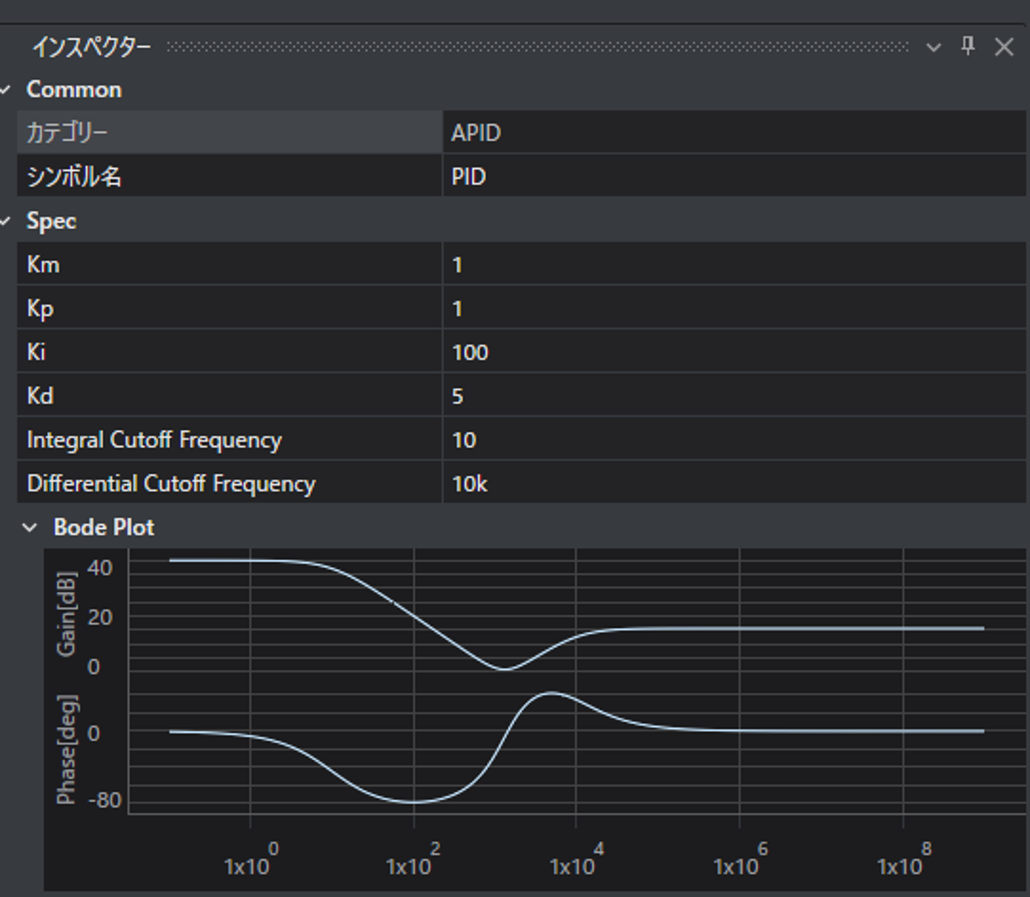
pythonで出力したボード線図と、インスペクターに表示されているボード線図が一致していることがわかります。
一巡伝達関数について
一巡伝達関数とは、補償器と主回路をまとめた伝達関数のことです。
補償器および主回路の伝達関数をそれぞれ$H(s)$、$P(s)$と表す時、一巡伝達関数$G(s)$は以下の式の通りとなります。
$$G(s) = P(s)H(s)$$
主回路に相当する降圧型コンバータの設計は第2回のスイッチング電源解析のための伝達関数で行っておりますので、
先ほど作成した補償器と併せて、実際に一巡伝達関数として解いてみましょう。
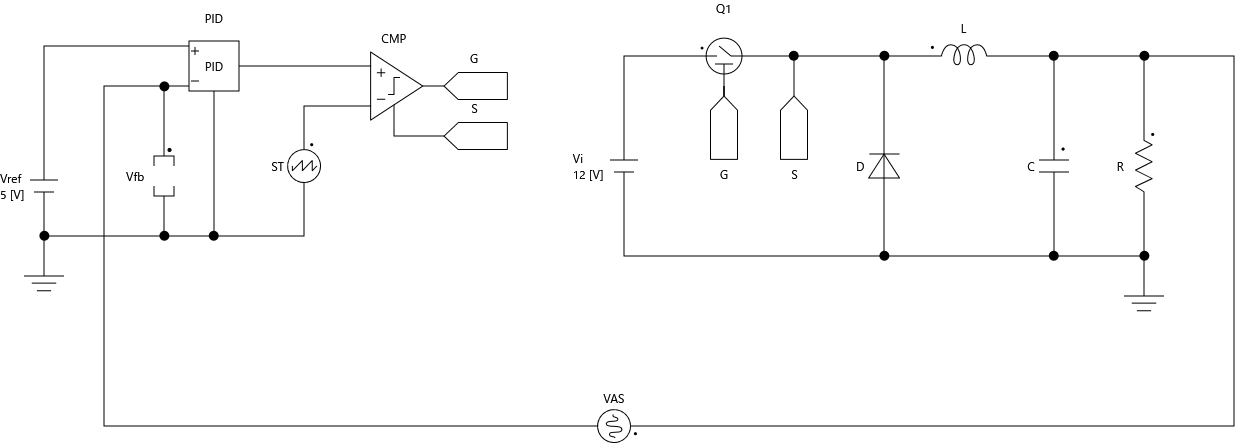
今回は降圧型コンバータを主回路として、その出力電圧を補償器であるPID制御に入力して、主回路の時比率$D$を生成することを考えます。
降圧型コンバータの時比率$D$に対する出力電圧$Vo$の伝達関数は、前回導出した式から以下のようになります。
$$\begin{aligned}
\frac{\Delta \hat{V_o}(s) }{ \Delta D(s)}
=\frac{ -(r_s – r_d) I_L + V_i }
{ LCs^2 + \frac{L + ((r_s – r_d)D + r_d)RC}{R}s + \frac{(r_s – r_d)D + r_d + R}{R} }\end{aligned}$$
先述通り、一巡伝達関数は主回路と補償器の伝達関数の積です。
ボード線図においてはゲインは[dB]で表示しているので、足し合わせることで一巡伝達関数として導出できます。
では、作成したPIDの伝達関数とコンバータの伝達関数を足し合わせた一巡伝達関数が、Scideamの周波数解析の結果と一致するか確認してみましょう。
一巡伝達関数のボード線図
まずは、pythonにてボード線図を作成します。
下のコードを用いることで、補償器と降圧型コンバータの伝達関数を足し合わせたボード線図を確認することができます。
この時、補償器の設定値は先程の値を使い、降圧型コンバータの設定値は以下の値を使用します。
| 変換名 | 値 | |
|---|---|---|
| 1 | 入力電圧 Vi | 12[V] |
| 2 | 負荷抵抗 R | 2.5[Ω] |
| 3 | リアクタンス L | 100[uH] |
| 4 | キャパシタンス C | 100[uF] |
| 5 | 時比率 D | 0.5 |
| 6 | スイッチの内部抵抗 rs | 0.1[Ω] |
| 7 | ダイオードの内部抵抗 | 0.1[Ω] |
import numpy as np, math
import matplotlib.pyplot as plt
from scipy import signal
#BuckConv
IL = 1
D = 0.5
rs = 0.1
rd = 0.1
Vi = 12
R = 2.5
L = 100 * 1e-6
C = 100 * 1e-6
num_Conv = np.array([(-(rs-rd)*IL + Vi)/((L*C))])
den_Conv = np.array([1, (L+((rs-rd)*D+rd)*R*C)/(R*L*C), ((rs-rd)*D+rd+R)/(R*L*C)])
#PID
Km = 1
Kp = 1
Ki = 100
Kd = 5
fi = 10
fd = 10**4
a = 2 * math.pi * fi
b = 2 * math.pi * fd
num_PID = np.array([(Kp+Kd)*Km, (Kp*(a+b)+Kd*a+Ki*a)*Km, (Kp*a*b + Ki*a*b)*Km])
den_PID = np.array([1,a+b,a*b])
freq = np.logspace(1, 5, 10000)
FRA_PID = signal.TransferFunction(num_PID*-1, den_PID)
FRA_Conv = signal.TransferFunction(num_Conv, den_Conv)
num_Loop = np.polymul(FRA_PID.num, FRA_Conv.num)
den_Loop = np.polymul(FRA_PID.den, FRA_Conv.den)
FRA_Loop = signal.TransferFunction(num_Loop, den_Loop)
# Plot
w, mag1, phase1 = signal.bode(FRA_PID,freq*2*np.pi)
w, mag2, phase2 = signal.bode(FRA_Conv,freq*2*np.pi)
w, mag3, phase3 = signal.bode(FRA_Loop,freq*2*np.pi)
plt.figure(figsize=(8,8))
plt.subplot(2,1,1)
plt.xlim(10,2e4)
plt.semilogx(freq,mag3)
plt.ylabel('Gain [dB]')
plt.grid()
plt.grid(True, which='both', axis='x', linestyle='--', linewidth=0.25, color='gray')
plt.subplot(2,1,2)
plt.xlim(10,2e4)
plt.semilogx(freq, phase3)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Phase [deg]')
plt.grid()
plt.grid(True, which='both', axis='x', linestyle='--', linewidth=0.25, color='gray')
ただし、本回路の補償器の入力は負帰還のため、補償器の伝達関数に-1をかけています。
では、回路と補償器を足し合わせた伝達関数をボード線図としてプロットしましょう。
今回も動作周波数は100[kHz]とします。
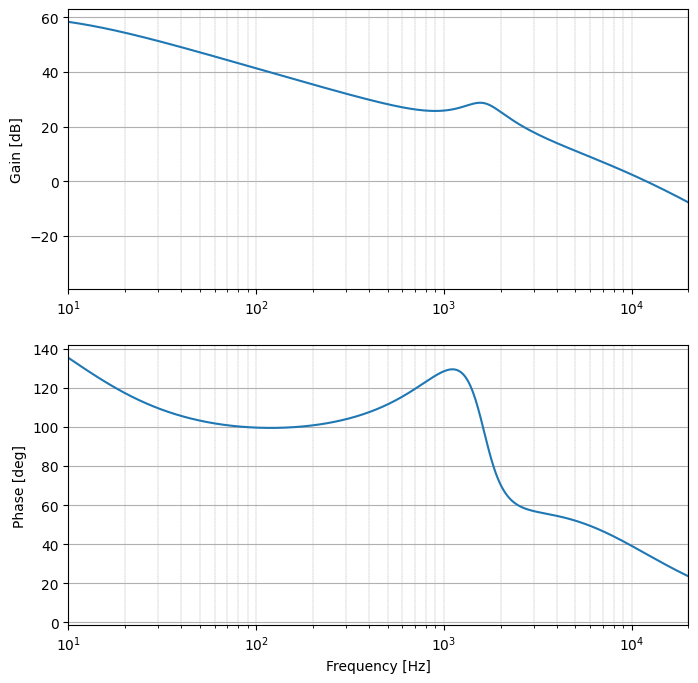
次に、Scideamで確認しましょう。
前回使用した降圧型コンバータの回路にPIDブロックを接続し、FRA解析を行います。
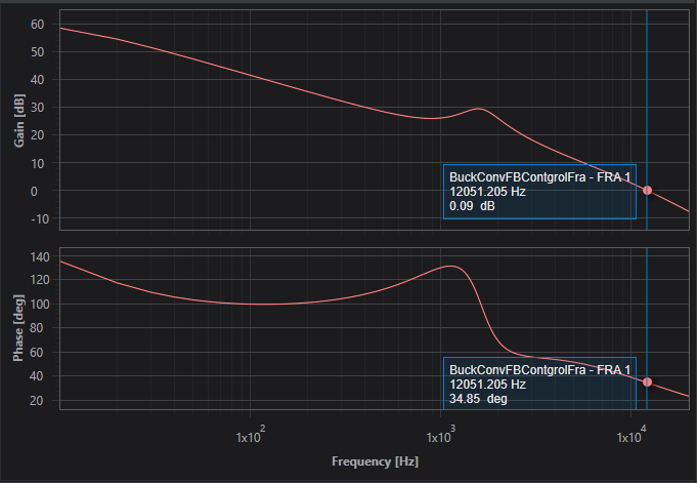
一巡伝達関数を式で解いた結果とScideamによるFRA解析結果が一致していることがわかります。
安定性の判断
さて、今までボード線図を確認してきましたが、そもそもボード線図から何がわかるのかとお思いの方もいらっしゃるでしょう。
結論を言えば、ボード線図によってその制御の安定性を確認することができます。
位相余裕とゲイン余裕について
安定性は判断する際に確認する項目として、位相余裕とゲイン余裕があります。
位相余裕
・ ゲインが0[dB]の時の位相の値で0[deg] ※に対して、どれくらい余裕があるかという指標です。
・ 位相が0[deg]を下回った時、発振する可能性があります。
・ 今回の例では30[deg]以上あればよいでしょう。
ゲイン余裕
・ 位相0[deg]の時のゲインの値が0[dB]に対して、どれくらい余裕があるかという指標です。
・ ゲインが0[dB]以上の時、発振する可能性があります。
以上の判断基準を元に、出力したボード線図を確認しましょう。
※ 下図において、一般的な一巡伝達関数$G$($s$)$H$($s$)は、図に赤字で示されている負号が反映されていないため、
位相余裕の基準は-180°となります。

これに対して、Scideamで定義している一巡伝達関数の解析は、負号も含まれているので位相余裕の基準は-360°
となります。
さらに、Scideamでは位相余裕を確認しやすいよう、360°を足した0°を基準としています。
そのため、一般的な位相余裕の基準とは180°の差があることにご注意ください。
詳細は弊社のヘルプセンターをご確認ください。
▼Scideam ヘルプセンター
FRA – Scideam HELP CENTER
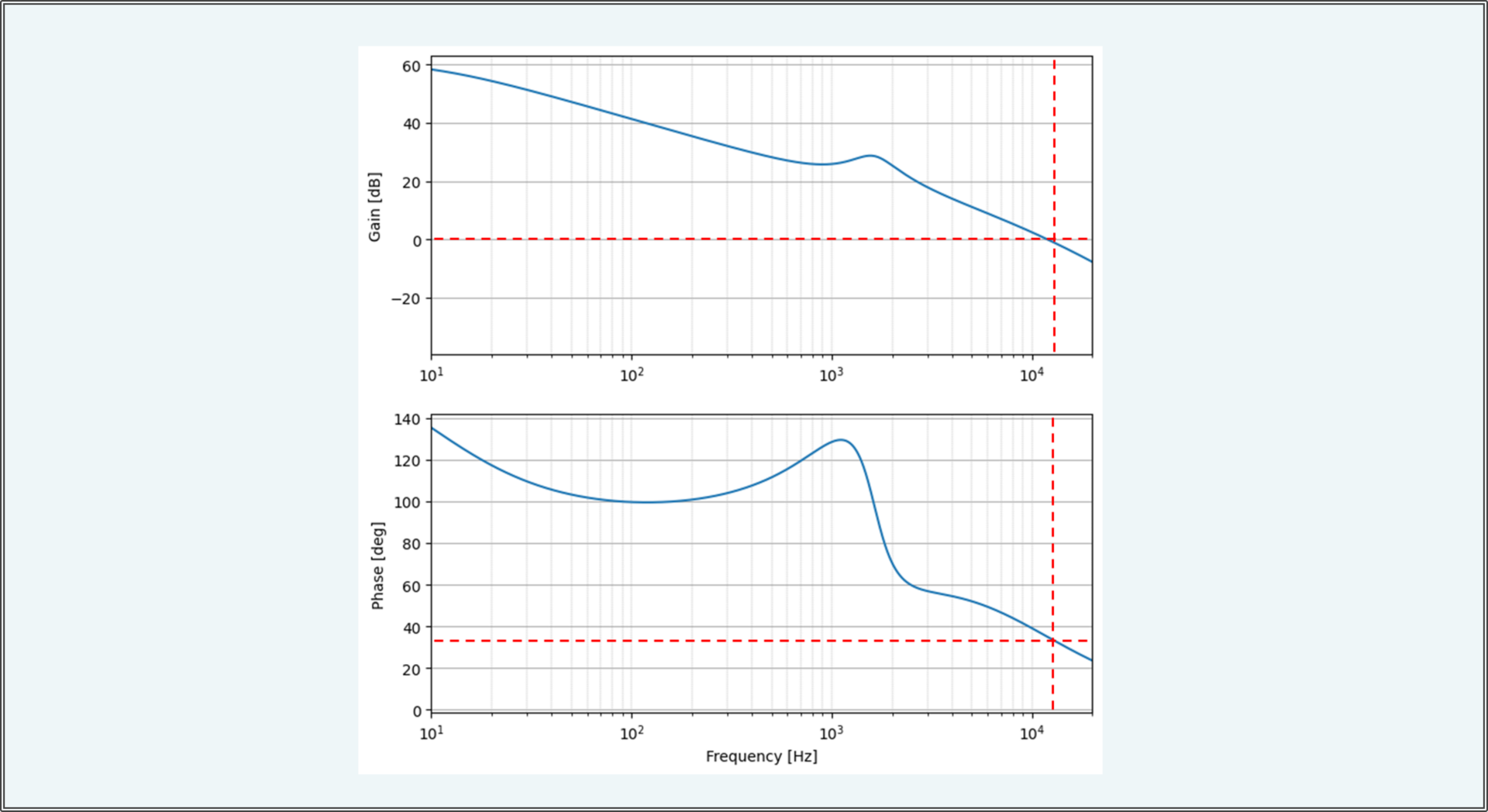
位相余裕の確認
Scideamで取得したボード線図で、位相余裕を確認しましょう。
表示している値を確認すると、ゲインがおよそ0[dB]の時、位相は34.85[deg]です。
したがって、今回設計した制御は安定していると判断できます。
ゲイン余裕の確認
次に、ゲインの余裕について確認してみましょう。
再度ボード線図を確認すれば、位相は0[deg]よりも高い位置までしか表示していませんが、周波数の最高値20[kHz]における位相がおよそ20[deg]の時点ですでにゲインが0[dB]を下回っているので、ゲイン余裕についても十分にあると判断できます。
おわりに
本ブログは今回で第3回となりますが、第1回に提示しました2つの目標
- スイッチング電源を数式的に解くためには、どのようにすればよいか
- 特性を考えるためにはどのようにすればよいか
につきまして、皆様ご理解いただけましたでしょうか。
これまでの数式や考え方はスイッチング電源を設計、検討する上での基本であり重要な知識になります。
特に、今回の一巡伝達関数の考え方、前回の小信号モデルの考え方は、周波数特性をうまく得られない時に確認する項目としても有効です。
これまでのブログ連載が設計者の皆様の一助となれば幸いです。
本文監修:中原正俊、中村創一郎
▼関連投稿 -コンバータ解析の始め方ー




