スイッチング電源解析のための
状態平均化法とは

コンバータ解析の始め方　第１回

はじめに

スイッチング電源は、スイッチが高速にON・OFFを繰り返すことで電力を制御しますが、このスイッチング動作をそのまま解析すると、非線形かつ時間変動するシステムとなり、解析が非常に複雑になります。

そこで、このスイッチの動作を平均化して一つの式として表し、われわれにも分かりやすい形に表現した方法が、状態平均化法です。
状態平均化法を用いると簡単かつ、精度の高い解析をすることが可能になります。

スイッチング電源を数式的に解くためには、どのようにすればよいか。

特性を考えるためにはどのようにすればよいか。

このブログ連載では、スイッチング電源を数式モデルとして表し、伝達関数を求め、最終的に周波数特性解析を行います。

シミュレーションモデルや回路シミュレータの解析方法など考えるときに役に立ちますので、これから電源解析を行う方、シミュレーションを始める方の参考になれば幸いです。

状態平均化法とは

スイッチング電源のような、複数の回路方程式が成り立つ回路の場合、解を求めるのに煩雑かつ複雑な計算が必要になります。状態平均化法は、それらの式を一つにすることができる手法です。

状態平均化法は値ではなく、方程式が平均化されていますので、実際に方程式を解いた場合と近しい値を得ることができます。

但し、スイッチング周波数が回路の共振周波数よりも十分に高い必要があります。
具体的な説明は割愛させていただきますが、設定するスイッチング周波数は、共振周波数に対して、100倍程度余裕を持たせるとよいでしょう。

状態方程式

状態方程式とは、名前の通り、ある条件に対する状態を数式の形にしたもので、現象や制御といった幅広い範囲に適用できます。

スイッチング電源の場合は回路方程式を当てはめることができます。
状態方程式は以下の式で表されます。

$$\frac{d{X}}{dt} = A{X} + B{U}$$

ここで、各変数ベクトルは以下のように定義されます。

X= 状態変数ベクトル
U = 変数ベクトル
A、B = 係数行列ベクトル

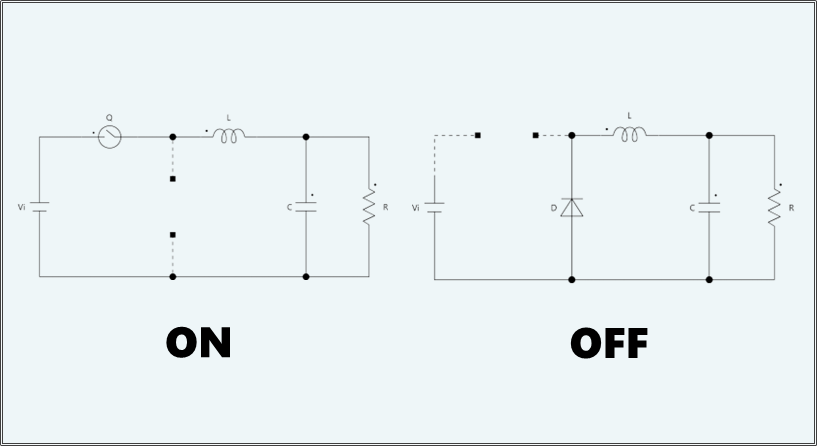
今回は下図のような降圧型コンバータの状態方程式を考えてみましょう。

状態平均化法

状態平均化法によれば、各状態の係数行列ベクトルにそれぞれの時比率をかけた値を足し合わせることができます。

降圧型コンバータはスイッチのON、OFFの２つの状態がありますので、スイッチのON時間、OFF時間の比率を $D$ とした時、
以下の式を立てることができます。

$$\hat{A} = A_{ON} D + A_{OFF} D’$$
$$\hat{B} = B_{ON} D + B_{OFF} D’$$
$$D’ = 1 – D$$

状態方程式を立てる

前項の状態方程式、及び状態平均化法の考えより、降圧型コンバータのONの時の状態方程式、OFFの時の状態方程式を考えてみましょう。

手順１　スイッチがONの時

スイッチがONの時、下記回路のようにあらわすことができます。
下記図の$rs$はスイッチのON抵抗です。
また、ON時にはダイオードは逆バイアスとなりますので、オープンとして扱います。

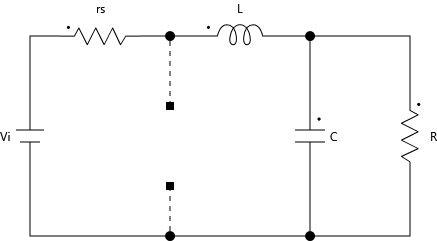
オームの法則、キルヒホッフの法則から上図回路は以下の式で表すことができます。

$$L \frac{d i_L}{d t} = -r_si_L – v_C + V_i$$

$$\frac{d i_{L}}{dt} = – \left( \frac{r_s i_{L}}{L} + \frac{v_{C}}{L} \right) + \frac{V_i}{L}$$

導出した式を移行して、以下のように変形します。

$$\begin{aligned}C \frac{d v_C}{dt} = -\frac{v_C}{R} + i_L\end{aligned}$$
$$\frac{d v_{C}}{dt} =\frac{i_{L}}{C} – \frac{v_{C}}{RC}$$

$$\frac{d}{dt} \left[ \begin{matrix} i_{L} \\ v_{C} \end{matrix} \right]= \left[ \begin{matrix} -\frac{r_s}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right]\left[ \begin{matrix} i_{L} \\ v_{C} \end{matrix} \right]+ \left[ \begin{matrix} \frac{1}{L} \\ 0 \end{matrix} \right] V_i$$

この時、状態方程式と照らし合わせると、$A_{\text{ON}}$、$B_{\text{ON}}$は以下の値となります。

$$\begin{aligned}A_{\text{ON}} = \left[ \begin{matrix} -\frac{r_s}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right] \\ B_{\text{ON}} = \left[ \begin{matrix} \frac{1}{L} \\ 0 \end{matrix} \right] \end{aligned}$$

手順２　スイッチがOFFの時

スイッチがOFFの時は下記回路のようにあらわすことができます。
スイッチ部がオープンになるため、電源である $Vi$ による電圧はかからないことが見て取れます。
また、ダイオードは順方向バイアスがかかるため、抵抗 $rd$ として扱います。

スイッチONの時と同様にて式を立てます。

$$\begin{aligned}L\frac{d i_{L}}{dt} = -r_d i_{L} – v_{C}\\\frac{d i_{L}}{dt} = -\frac{r_d i_{L}}{L} – \frac{v_{C}}{L}\end{aligned}$$

$$\begin{aligned}C\frac{d v_{C}}{dt} = i_{L} – \frac{v_{C}}{R}\\\frac{d v_{C}}{dt} = \frac{i_{L}}{C} – \frac{v_{C}}{RC}\end{aligned}$$

$$\frac{d}{dt} \left[ \begin{matrix} i_{L} \\ v_{C} \end{matrix} \right]= \left[ \begin{matrix} -\frac{r_d}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right]\left[ \begin{matrix} i_{L} \\ v_{C} \end{matrix} \right]$$

この時、状態方程式と照らしあらせると、$A_{\text{OFF}}$、$B_{\text{OFF}}$は以下の値となります。
$$\begin{aligned}A_{\text{OFF}} = \left[ \begin{matrix} -\frac{r_d}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right]\end{aligned}$$
$$\begin{aligned}B_{OFF} = \left[\begin{matrix} 0 \\ 0 \end{matrix} \right]\end{aligned}$$

手順３　平均化する

前項までに求めたスイッチのON、OFFの係数行列ベクトル$A$、$B$を、はじめに示した、$\hat{A}$、$\hat{B}$の式に代入しましょう。

$$\begin{aligned}\hat{A}= \left[ \begin{matrix} – \frac{r_s}{L} & -\frac{1}{L}\\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right] D+ \left[ \begin{matrix} -\frac{r_d}{L} & -\frac{1}{L}\\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right] D’\\=\left[　\begin{matrix}-\frac{r_sD + r_dD’}{L} & -\frac{1}{L}\\ \frac{1}{C} & -\frac{1}{RC}\end{matrix} \right]\end{aligned}$$

$$\hat{B} = \left[ \begin{matrix} \frac{1}{L} \\ 0 \end{matrix} \right] D+ \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right] D’= \left[ \begin{matrix} \frac{D}{L} \\ 0 \end{matrix} \right]$$

各状態方程式の$\hat{X}$、$\hat{U}$に該当する値は下記式となります。

$$\begin{aligned}\hat{X} = \left[ \begin{matrix} i_L \\ v_C \end{matrix} \right]\\
\hat{U} = V_i\end{aligned}$$

以上より、降圧型コンバータの状態平均化方程式は以下の式で示されます。

$$\frac{d}{dt}\left[\begin{matrix} i_L \\ v_C \end{matrix} \right]= \left[ \begin{matrix} -\frac{(r_s – r_d)D + r_d}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right]\left[ \begin{matrix} i_L \\ v_C \end{matrix} \right]+ \left[ \begin{matrix} \frac{D}{L} \\ 0 \end{matrix} \right] V_i$$

おわりに

今回は状態平均化法を用いて、降圧型コンバータの状態平均化方程式を導出しました。

次回は状態平均化方程式を使用して、降圧型コンバータの周波数特性を確認します。

参考

【制御の概要】
いまさら聞けないデジタル電源超入門　 第１回 概要編

【周波数特性について】
いまさら聞けないデジタル電源超入門　 第６回 デジタル制御 ①

【使用した回路】
周波数特性解析編 – Scideam HELP CENTER

【文献】
スイッチングコンバータの基礎　コロナ社

本文監修：中原正俊、中村創一郎

▼関連投稿