スイッチング電源解析のための
伝達関数
コンバータ解析の始め方 第2回
目次
はじめに
状態平均化法編では降圧型コンバータの状態平均化方程式を導出しました。
今回は降圧型コンバータの伝達関数を確認してみましょう。
▼ 前回:スイッチング電源電源解析のための状態平均化法とは
状態方程式のおさらい
前回導出した降圧型コンバータの状態平均化方程式は以下の通りです。
$$\frac{d \hat{X}}{dt} = \hat{A}\hat{X} + \hat{B} \hat{U}$$
$$\frac{d}{dt}\left[ \begin{matrix} i_L \\ v_C \end{matrix} \right]= \left[ \begin{matrix} -\frac{ (r_s – r_d)D + r_d}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right]\left[ \begin{matrix} i_L \\ v_C \end{matrix} \right]+ \left[ \begin{matrix} \frac{D}{L} \\ 0 \end{matrix} \right] V_i$$
伝達関数とは
フーリエ変換の考えでは、すべての波形は周波数の異なる正弦波の重ね合わせによって再現することが可能です。
つまり、ある時間における入力と出力の各周波数成分を比較することで、その入出力間の周波数特性を知ることができます。
このように、入出力の関係を周波数領域で表した関数を伝達関数と呼びます。
入力とする値は任意ではありますが、スイッチング電源であれば、スイッチのオンオフのタイミングである時比率$D$を入力とすることが多いです。
したがって、今回は時比率を入力としたときの降圧型コンバータの伝達関数を求めましょう。
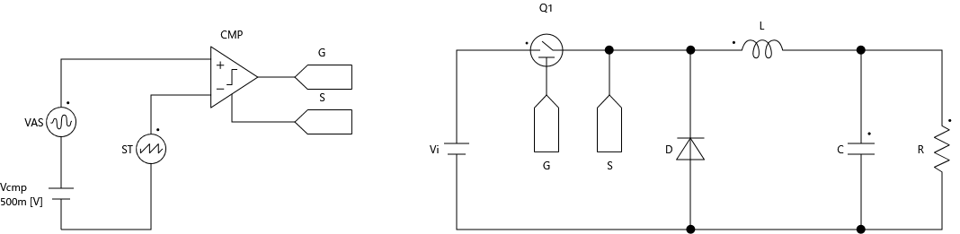
ここで、時比率Dを任意の値に調節できるよう、PWM制御を追加します。
PWMについては、いまさら聞けなるデジタル電源超入門 第4回 PWM編をご一読ください。
【図】降圧型コンバータのモデル図
上記回路は、スイッチに与える時比率を固定値+微小信号で決定しています。
このように、制御対象に入力される値が外部で決定するような構成をオープンループと呼びます。
また、オープンループとは異なり、出力された値を入力にフィードバックするような構成をクローズドループと呼びます。
フィードバックする値は補償器を通して、次の入力を制御するために使用されることが多いです。
制御部まで含めた伝達関数は一巡伝達関数と呼ばれますが、こちらは次のブログ記事で説明したいと思います。
前置きが長くなってしまいましたが、伝達関数の導出を始めましょう。
伝達関数を求めるにあたり、二つの状態の特性を考えます。
静特性の確認
DCスイッチング電源は、基本的には動作初期の出力は不安定ですが、時間の経過とともに収束し、一定の値になります。
この状態を定常状態と呼び、この時の特性を定常特性、または静特性と呼びます。
静特性は時間による出力の変化量が0と考えられますので、以下の式のように表せます。
$$\begin{aligned}\frac{d \hat{X}}{dt} = \hat{A}\hat{X} + \hat{B} \hat{U} = 0\end{aligned}$$
ここで、静特性時の出力変数ベクトルを以下のように定義し、出力変数を求める式に変形しましょう。
$$\begin{aligned}\hat{X_s} = \left[ \begin{matrix} I_d \\ V_c \end{matrix} \right]= -\hat{A}^{-1} \hat{B} \hat{U}\end{aligned}$$
降圧型コンバータの状態方程式から各値を代入すると以下のようになります。
$$\begin{align}-\hat{A}^{-1} \hat{B} \hat{U}&=-\frac{RLC}{{(r_s – r_d)D + r_d} + {R}}\left[ \begin{matrix}\frac{1}{RC} & \frac{1}{L} \\ -\frac{1}{C} & -\frac{ (r_s – r_d)D + r_d}{L}\end{matrix} \right]\left[ \begin{matrix} \frac{D}{L} \\ 0 \end{matrix} \right]V_i\\&=-\frac{DV_i}{(r_s – r_d)D + r_d + R}\left[ \begin{matrix} 1 \\ -R \end{matrix} \right]\end{align}$$
この式から、降圧型コンバータの静特性の出力を確認する事ができます。
動特性の確認
動特性は定常状態ではない時、つまり、時間によって値が変化する際の特性です。
今回は、制御によって降圧型コンバータの時比率$D$を変化させる場合を考えてみましょう。
微小信号
入力とする変数にもよりますが、変化量は微小信号で考える場合が多いです。
これは、非線形項が存在する場合、後述するラプラス変換の考え方を適用できないためです。
では、実際に状態方程式を変形させながら、非線形項が存在しないか確認してみましょう。
まず、変化量を$Δ$で表すと、状態方程式は下記のようになります。
$$\begin{aligned}\frac{d}{dt} (\hat{X} + \Delta \hat{X})=& (\hat{A} + \Delta \hat{A})(\hat{X} + \Delta \hat{X})+ (\hat{B} + \Delta \hat{B}) V_i\\=& \hat{A} \hat{X} + \Delta \hat{A} \hat{X}+ \hat{A} \Delta \hat{X} + \Delta \hat{A} \Delta \hat{X}+ \hat{B} Vi + \Delta \hat{B} V_i\end{aligned}$$
上記式のうち、$Δ$を含まない項は、元々の状態方程式ですので消去します。
$$\begin{aligned}\frac{d}{dt} \Delta \hat{X}=\Delta \hat{A} \hat{X}+ \hat{A} \Delta \hat{X} + \Delta \hat{A} \Delta \hat{X}+ \Delta \hat{B} V_i\end{aligned}$$
ここで、扱っている回路はクローズドループであるとして考えてみます。
この場合、出力された値$Δ\hat{X}$を入力にフィードバックし、その入力値は$Δ\hat{A}$へ代入されます。
つまり、$Δ\hat{A}$と同等の式を出力値$\hat{X}$は含んでおり、$Δ\hat{A}Δ\hat{X}$は非線形項であると判断できます。
先述の通り、非線形項を含む場合には状態方程式を解くことができません。
では、変化量を微小信号として考えるとどうでしょうか。
微小信号は十分に小さい値ですから、その変化量の積である$Δ\hat{A}Δ\hat{X}$も他の項と比較して十分に小さいです。
そのため、$Δ\hat{A}Δ\hat{X}$を無視することができ、 式から非線形項をなくすことができます。
$$\frac{d}{dt} \Delta \hat{X}= \Delta \hat{A} \hat{X} + \hat{A} \Delta \hat{X}+ \Delta \hat{B} V_i$$
反対に非線形項がない、または、微小信号とみなさずとも十分に小さい値である場合には、微小信号として考えずにも解くことは可能ですが、単純に項が減ることを加味すれば、微小信号で考えて損はないでしょう。
ラプラス変換する
先に示した式をラプラス変換してみましょう。ここで、$I$は単位行列です。
$$sI \Delta \hat{X}(s)= \Delta \hat{A}(s) \hat{X} + \hat{A} \Delta \hat{X}(s)+ \Delta \hat{B}(s) V_i$$
出力$Δ\hat{X}$についての式にするため、右辺の$\hat{A}Δ\hat{X}$を左辺へ移行しましょう。
この時、$\hat{A}$は正方行列ですので、値は逆行列となります。
$Δ\hat{A}$、$Δ\hat{B}$を偏微分して、$ΔD$の項に整理すると以下の式になります。
$$\begin{align}\Delta \hat{X}(s)&= (sI – \hat{A})^{-1}(\Delta \hat{A}(s) \hat{X} + \Delta \hat{B}(s) V_i)\\&= (sI – \hat{A})^{-1}\left(\frac{\partial \hat{A}} {\partial D}\Delta D(s) \hat{X}+ \frac{\partial \hat{B}}{\partial D}\Delta D(s) V_i\right)\\&= (sI – \hat{A})^{-1}\left(\frac{\partial \hat{A}}{\partial D} \hat{X}+ \frac{\partial \hat{B}}{\partial D} \hat{Y}\right)\Delta D(s)\end{align}$$
伝達関数を求める
今回の入力とする値は時比率$D$です。では、時比率が変化した際の出力$ΔX$を考えましょう。
先述の式を変形させて下記の式の形にします。
$$\frac{\Delta \hat{X}}{\Delta D}=(sI – \hat{A})^{-1}(\frac{\partial \hat{A}}{\partial D} \hat{X}+ \frac{\partial \hat{B}}{\partial D} \hat{Y})$$
各項を整理しましょう。 それぞれの項を計算した値は以下の通りです。
$$\begin{align}\left( sI – \hat{A} \right)^{-1}
&=\frac{1}{ s^2 + \frac{L + ((r_s – r_d)D + r_d)RC}{RLC}s + \frac{(r_s – r_d)D + r_d + R}{RLC} }\left[ \begin{matrix} \frac{RCs+1}{RC} & -\frac{1}{L}\\\frac{1}{C} & \frac{sL + (r_s – r_d)D + r_d}{L} \end{matrix} \right]\end{align}$$
$$\frac{\partial \hat{A} }{\partial D} \hat{X}=\frac{\partial}{\partial D} \left[ \begin{matrix} -\frac{(r_s – r_d)D + r_d}{L} & -\frac{1}{L} \\ \frac{1}{C} & -\frac{1}{RC} \end{matrix} \right]\left[ \begin{matrix} {I_L} \\ {V_C} \end{matrix} \right]=\left[ \begin{matrix} -\frac{r_s – r_d}{L} & 0 \\ 0 & 0 \end{matrix} \right]\left[ \begin{matrix} {I_L} \\ {V_C} \end{matrix} \right]=\left[ \begin{matrix} -\frac{r_s – r_d}{L}I_L \\ 0 \end{matrix} \right]$$
$$\frac{\partial \hat{B}}{\partial D} \hat{Y}
=\frac{\partial}{\partial D}
\left[ \begin{matrix} \frac{D}{L} \\ 0 \end{matrix} \right] V_i
=\left[ \begin{matrix} \frac{V_i}{L} \\ 0 \end{matrix} \right]$$
$$\left(\frac{\partial \hat{A}}{\partial D} \hat{X}+ \frac{\partial \hat{B}}{\partial D} \hat{Y}\right)
=\left[ \begin{matrix} -\frac{r_s – r_d}{L}I_L \\ 0 \end{matrix} \right]
+ \left[ \begin{matrix} \frac{V_i}{L} \\ 0 \end{matrix} \right]
=\left[ \begin{matrix} \frac{-(r_s – r_d) I_L + V_i}{L} \\ 0 \end{matrix} \right]$$
上記の結果を代入すると、時比率$D$を入力とした際の降圧型コンバータの伝達関数は以下のようになります。
$$\begin{align}
\frac{\Delta \hat{X}(s) }{ \Delta D(s)}
&=\frac{1}{ s^2 + \frac{L + ((r_s – r_d)D + r_d)RC}{RLC}s + \frac{(r_s – r_d)D + r_d + R}{RLC} }
\left[ \begin{matrix} \frac{RCs+1}{RC} & -\frac{1}{L}\\
\frac{1}{C} & \frac{sL + (r_s – r_d)D + r_d}{L} \end{matrix} \right]
\left[ \begin{matrix} \frac{-(r_s – r_d) I_L + V_i}{L} \ 0 \end{matrix} \right]\\
&=\frac{ -(r_s – r_d) I_L + V_i }
{s^2 + \frac{L + ((r_s – r_d)D + r_d)RC}{RLC}s + \frac{(r_s – r_d)D + r_d + R}{RLC} }
\left[ \begin{matrix}
\frac{RCs+1}{RLC}\\ \frac{1}{LC}
\end{matrix} \right]
\end{align}$$
伝達関数の確認する
それでは、導出した伝達関数から、どのような特性を得られるか確認してみましょう。
各値を以下のように設定して、Pythonを活用して周波数特性をプロットしてみます。
| 変数名 | 値 | |
|---|---|---|
| 1 | 入力電圧 Vi | 12[V] |
| 2 | 負荷抵抗 R | 2.5[Ω] |
| 3 | リアクタンス L | 100[uH] |
| 4 | キャパシタンス C | 100[uF] |
| 5 | 時比率 D | 0.5 |
| 6 | スイッチの内部抵抗 rs | 0.1[Ω] |
| 7 | ダイオードの内部抵抗 rd | 0.1[Ω] |
使用したコードは以下の通りです。
import numpy as np, math
import matplotlib.pyplot as plt
from scipy import signal
IL = 1
D = 0.5
rs = 0.1
rd = 0.1
Vi = 12
R = 2.5
L = 100 * 1e-6
C = 100 * 1e-6
num = [(-(rs-rd)*IL + Vi)/((L*C))]
den = [1, (L+((rs-rd)*D+rd)*R*C)/(R*L*C), ((rs-rd)*D+rd+R)/(R*L*C)]
func1 = f"{round(num[0],0)}"
func2 = f"{round(den[0],0)}s^2 + {round(den[1],0)}s + {round(den[2],0)}"
print(f" 伝達関数は: {func1} / {func2}")
FRA_PID = signal.TransferFunction(num, den)
freq = np.logspace(1, 5, 10000)
w, mag, phase = signal.bode(FRA_PID,2*np.pi*freq)
plt.figure(figsize=(8,8))
plt.subplot(2,1,1)
plt.xlim(10, 2e4)
plt.semilogx(freq,mag)
plt.ylabel('Gain [dB]')
plt.grid()
plt.grid(True, which='both', axis='x', linestyle='--', linewidth=0.25, color='gray')
plt.subplot(2,1,2)
plt.xlim(10, 2e4)
plt.semilogx(freq, phase)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Phase [deg]')
plt.grid()
plt.grid(True, which='both', axis='x', linestyle='--', linewidth=0.25, color='gray')
plt.show()
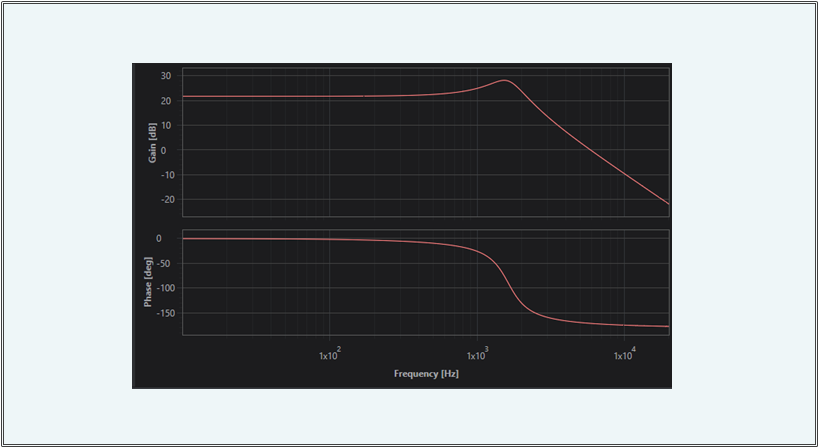
上記のプログラムを動作させると以下のような特性を得ることができます。
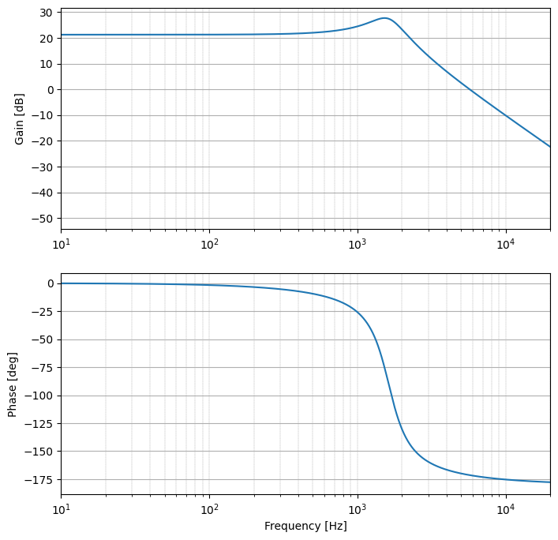
Scideamでも確認してみましょう。
冒頭で紹介した回路で周波数特性解析を行うと以下の特性を得ることができます。
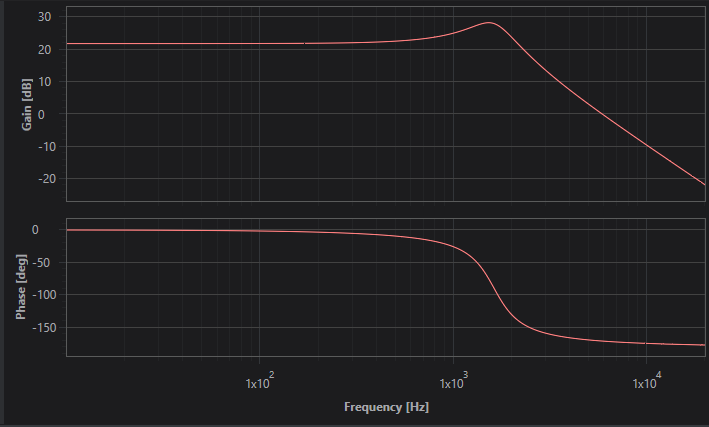
2つの波形を比較すると、およそ同じ波形となることがわかります。
今回比較した2つの方法による、ボード線図を表示するまでに必要な設定をまとめると以下のようになります。
- Python:状態方程式から伝達関数の導出、パラメータ設定
- Scideam:回路構成と各パラメータ、解析する周波数範囲
※pythonは上記のコードを使用した場合になります。
伝達関数とシミュレータの比較
伝達関数は数式で表されるため、入力の変化による出力への影響度を数値として確認することができます。
しかし、降圧型コンバータのような簡単な回路でも、伝達関数を導出が簡単でないことは、これまでの内容で実感いただけたかと思います。
複雑な回路の伝達関数を解こうとすれば、その導出はさらに困難となるでしょう。
Scideamをはじめとする回路シミュレータは、回路方程式を自動的に立ててその特性を解析します。
そのため、煩雑な回路方程式やそこから発展させる伝達関数の導出をする手間をなくすことが可能です。
選択した解法や解析時間、回路規模、パラメータ設定などによっては、解析時間が遅くなることはありますが、
伝達関数を導出する場合と比較すれば、大幅な時間短縮が望めるでしょう。
おわりに
今回は、状態平均化方程式に続いて伝達関数を導出し、降圧型コンバータの周波数特性を確認しました。
実際の開発現場では回路シミュレータを使用する場合が多いと思いますが、数式的にどのように解くかを理解することで、モデルの改善にどのようなアプローチが必要か推測することができます。
シミュレータをより有効活用するためには、シミュレータに頼り切らず、作成した回路がどのような動作をするか理解することが重要となります。
Scideamは30日間、フルパッケージでお試しいただけます。
ヘルプセンターでは、チュートリアルの他、様々な回路に対するサンプルをご用意しております。
Scideamインストール後は是非、サンプル回路ページよりダウンロード頂き、様々な回路・解析をお試し下さい!
本文監修:中原正俊、中村創一郎
▼関連投稿 -コンバータ解析の始め方ー